-
[Python] 프로그래머스 / Level3 / 경주로 건설 (BFS, DP)코딩테스트 2021. 9. 4. 14:49
문제 : https://programmers.co.kr/learn/courses/30/lessons/67259
코딩테스트 연습 - 경주로 건설
[[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] 3800 [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] 2100 [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[
programmers.co.kr
😊 정답 코드
from collections import deque def solution(board): N = len(board) directions = [(-1,0), (0,-1), (1,0), (0,1)] # 상좌하우 def bfs(x,y,cost,d): graph = [[0]*N for _ in range(N)] for a in range(N): for b in range(N): if board[a][b] == 1 : graph[a][b] = -1 # 벽을 -1로 설정 q = deque() q.append((x,y,cost,d)) while q: x,y,cost,idx = q.popleft() for i in range(len(directions)): nx = x + directions[i][0] ny = y + directions[i][1] if nx < 0 or nx >= N or ny < 0 or ny >= N : continue if graph[nx][ny] == -1 : continue if idx == i : newcost = cost + 100 else : newcost = cost + 600 if graph[nx][ny] == 0 or ((graph[nx][ny] != 0) and graph[nx][ny] > newcost): q.append((nx,ny,newcost,i)) graph[nx][ny] = newcost else : continue return graph[N-1][N-1] return min(bfs(0,0,0,2),bfs(0,0,0,3))오늘은 정답 소스코드부터 올립니다.
굳이 벽을 -1로 설정할 필요는 없습니다.
🤒 나를 역대급으로 괴롭히신 분
BFS (Breadth First Search, 깊이 우선탐색)과 Dynamic Programming의 개념을 사용해야 한다는 것은 깨달았지만, 왜인지 테스트케이스 몇 개가 자꾸 삑이났다.
내가 짠 코드를 몇번이고 복기해도 어디서 틀렸는지 알 수가 없었다.
내용을 싹 출력해보기도 하고, 경건한 마음으로 손 디버깅도 해보고, 결국 이유를 찾아냈다.
Hand Debuging 🙄 오답 코드
from collections import deque def solution(board): N = len(board) directions = [(-1,0), (0,-1), (1,0), (0,1)] # 상좌하우 def bfs(x,y,d): graph = [[0]*N for _ in range(N)] for a in range(N): for b in range(N): if board[a][b] == 1 : graph[a][b] = -1 # 벽을 -1로 설정 q = deque() q.append((x,y,d)) while q: x,y,idx = q.popleft() for i in range(len(directions)): nx = x + directions[i][0] ny = y + directions[i][1] if nx < 0 or nx >= N or ny < 0 or ny >= N : continue if graph[nx][ny] == -1 : continue cost = 0 if idx == i : cost = graph[x][y] + 100 else : cost = graph[x][y] + 600 if graph[nx][ny] == 0 or (graph[nx][ny] != 0 and graph[nx][ny] > cost): q.append((nx,ny,i)) graph[nx][ny] = cost print('nx ny cost i /',nx,ny,cost,i) else : continue return graph[N-1][N-1] return min(bfs(0,0,2),bfs(0,0,3))🤔 틀린 이유
결론부터 말하자면, 정답코드와 오답코드의 차이는 "큐에 cost를 담느냐" , "graph[nx][ny]에 cost를 담느냐" 다.
문제를 해석하면 알겠지만 (같은 방향 -> 다른 방향) 이동 경우 600의 비용이 추가되고, (같은 방향 -> 같은 방향) 이동 경우 100의 비용이 추가된다. bfs(0,0,3)의 케이스로 이를 비교해보았다.
1. cost를 graph[nx][ny]에 담는경우
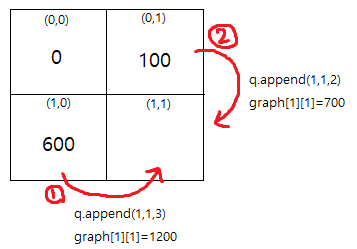
bfs((0,0,3))의 케이스 큐에 수많은 원소(노드)들이 담기겠지만, 다음의 두 상황을 비교해보자.
두 화살표를 고려할때 1번이 2번보다 빨리 큐에 담긴다. (상, 좌, 하, 우 의 순서로 큐를 담기 때문)
1번 화살표가 진행된 후, graph[1][1]=1200으로 업데이트된다. 큐에는 (1,1,3)이 담긴다. 3은 오른쪽을 의미한다.
2번 화살표가 진행된 후, graph[1][1]=700으로 업데이트된다. 큐에는 (1,1,2)가 담긴다. 2는 아래쪽을 의미한다.
후에, 큐에 담겼던 (1,1,3)이 처리될 것이다. 그 노드를 처리할 때, 오른쪽 (1,2)로 갈 수 있으므로
cost = graph[x][y] + 100의 코드가 실행된다.
기억해보면, (1,1,3)은 (1,0)(=600)에서 3(오른쪽)으로 온 노드이다. (1,0)(=600)은 위(0,0)에서 아래(방향 2)로 온 노드 이므로, 아래쪽 -> 오른쪽으로 방향 전환이 이루어졌기 때문에 (1,1)의 값이 1200로 설정 되었었다.
그러면 거기서 한번 더 같은 방향인 오른쪽(1,2)으로 가면 1200 + 100 = 1300이 되어야 할 것이다.
하지만 cost = graph[x][y] + 100이 실행되는 시점에서 graph[x][y] 는 이미 2번 화살표 때문에 700으로 변경되어있다. 이는 1300으로 이루어질 수 있는 엄청난 스노우볼의 씨앗을 틀어막는 것이다.
따라서 1300이 되어야 할 값이 700 + 100 = 800. 엉뚱한 값이 되는 상황이 벌어지는 것이다.
이를 방지하기 위해, graph[nx][ny]에 값을 업데이트 하는 것이 아니고 큐에 노드를 담을때마다 cost를 같이 담아야 한다.
2. cost를 큐에 담는 경우
위 그림의 1번 화살표에서 (1,1,1200,3) 이 큐에 담기게된다. 여기서 1200이라는 값은 노드안에 안전하게 담기게 되고, 후에 (1,1,1200,3)을 처리할때도 1200이라는 값이 보존 되어있기 때문에 1300이라는 값이 잘 나올 수 있게 된다.

'코딩테스트' 카테고리의 다른 글
[Python] 백준 / Gold / 1707 : 이분 그래프 (0) 2021.09.22 [Python] 백준 / Gold / 1520 : 내리막길 ( DFS + DP ) (0) 2021.09.18 [Python] 프로그래머스 / Level3 / 표 편집 (Linked List) (0) 2021.08.31 [Python] 알고리즘 풀이 팁 (0) 2021.08.27 [Python] 프로그래머스 / Level3 / 가장 먼 노드 (최단거리 알고리즘) (0) 2021.08.27